Courses
MDE-MET-01; Calculus and Linear Algebra for Graduate Students
Notebooks
Gram-Schmidt Algorithm

The Gram-Schmidt Process

This notebook is based upon the data presented here which is worth reading.

Begin by importing modules required

import matplotlib.pyplot as plt
import numpy as np
from scipy.linalg import norm

Setup grid for visualisation

s = np.linspace(-1, 1, 10)
t = np.linspace(-1, 1, 10)
S, T = np.meshgrid(s, t)

Define vectors the vectors

x1 = np.array([3, 6, 2])
x2 = np.array([1, 2, 4])
x3 = np.array([2, -2, 1])

Reshape data for visualisation

x1 = x1.reshape((-1, 1))
x2 = x2.reshape((-1, 1))
x3 = x3.reshape((-1, 1))

vec = np.array([
    np.hstack((np.zeros((1,3)), x1.T)),
    np.hstack((np.zeros((1,3)), x2.T)),
    np.hstack((np.zeros((1,3)), x3.T))
    ])

X = vec[0, :, 3] * S + vec[1, :, 3] * T
Y = vec[0, :, 4] * S + vec[1, :, 4] * T
Z = vec[0, :, 5] * S + vec[1, :, 5] * T

Set up plotting

fig = plt.figure(figsize = (7, 7))
ax = fig.add_subplot(projection='3d')
ax.plot_wireframe(X, Y, Z, linewidth=1.5, alpha=0.3)

colors = ['tab:red', 'tab:blue', 'tab:green']
s = ['$x_1$', '$x_2$', '$x_3$']
for i in range(vec.shape[0]):
    X, Y, Z, U, V, W = zip(*vec[i, :, :])
    ax.quiver(X, Y, Z, U, V, W, length=1, normalize=False,
              color=colors[i], alpha=0.6, arrow_length_ratio=0.08,
              pivot='tail', linestyles='solid', linewidths=3)
    ax.text(vec[i, :, 3][0], vec[i, :, 4][0], vec[i, :, 5][0], s=s[i], size=15)

ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_zlabel('$z$')

Now perform the Gram-Schmidt process for vectors $v_1=x_1$, $v_2$ and $v_3$

v1 = x1

proj_x2 = (x2@v1) / (v1@v1) * v1
v2 = x2 - proj_x2

proj_x3 = (x3@v1) / (v1@v1) * v1 + (x3@v2) / (v2@v2) * v2
v3 = x3 - proj_x3

Reshape for plotting

v1 = v1.reshape((-1, 1))
v2 = v2.reshape((-1, 1))
v3 = v3.reshape((-1, 1))

vec1 = np.array([
    np.hstack((np.zeros((1,3)), v1.T)),
    np.hstack((np.zeros((1,3)), v2.T)),
    np.hstack((np.zeros((1,3)), v3.T))
    ])

X1 = vec1[0, :, 3] * S + vec1[1, :, 3] * T
Y1 = vec1[0, :, 4] * S + vec1[1, :, 4] * T
Z1 = vec1[0, :, 5] * S + vec1[1, :, 5] * T

s1 = ['', '$v_2$', '$v_3$']
for i in range(vec1.shape[0]):
    X, Y, Z, U, V, W = zip(*vec1[i, :, :])
    ax.quiver(X, Y, Z, U, V, W, length=1, normalize=False,
          color=colors[i], alpha=0.6, arrow_length_ratio=0.08,
          pivot='tail', linestyles='dashed', linewidths=3)
    ax.text(vec1[i, :, 3][0], vec1[i, :, 4][0], vec1[i, :, 5][0], s=s1[i], size=15)

plt.show()

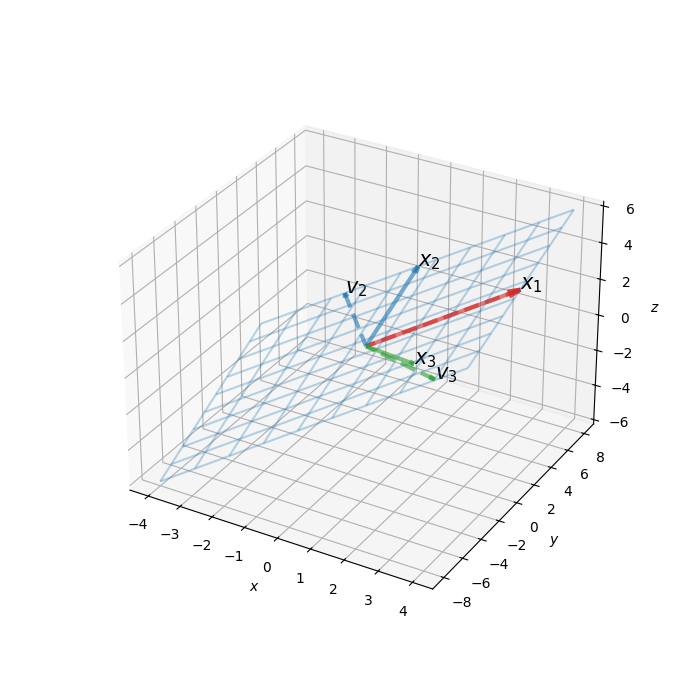
gram_schmidt

Normalize the orthogonal vectors

u1 = v1 / norm(v1)
u2 = v2 / norm(v2)
u3 = v3 / norm(v3)

U1 = np.vstack((u1, u2, u3)).T