Lagrange Polynomials
This notebook uses the scipy lagrange function to compute the Lagrange polynomial.
import numpy as np
from numpy.polynomial.polynomial import Polynomial
from scipy.interpolate import lagrange
import matplotlib.pyplot as plt
from IPython.display import Markdown as md
plt.style.use('seaborn-poster')
For some points $x$, define some data $y$ and create the Lagrange polynomial $f$, which has coefficients $p$
x = [0.0, 1.0, 2.0]
y = [1.0, 3.0, 2.0]
f = lagrange(x, y)
p = Polynomial(f.coef[::-1]).coef
z = ['' if i==0 else ('x' if (i==1) else 'x^{}'.format(i)) for i in np.arange(np.size(x))]
string= [str(p[i]) + str(z[i]) for i in np.arange(np.size(x))]
print(string)
md("Coefficients of the interpolating polynomial: {}".format(p))
['1.0', '3.5x', '-1.5x^2']
Coefficients of the interpolating polynomial: [ 1.0, 3.5, -1.5]
def lagrange_basis(x_int, y_int, x_new):
"""
This function takes pairs of points (x_int, y_int) and, from a set of points x_new
computes the Lagrange polynomial to return the interpolated values y_new
"""
l = np.zeros((np.size(x_int), np.size(x_new)), dtype=np.float32)
i = int(0)
for xi, yi in zip(x_int, y_int):
l[i,:] = np.prod( [(x_new - xj) / (xi - xj) for xj in x_int if xi != xj], axis=0)
i=i+1
return l
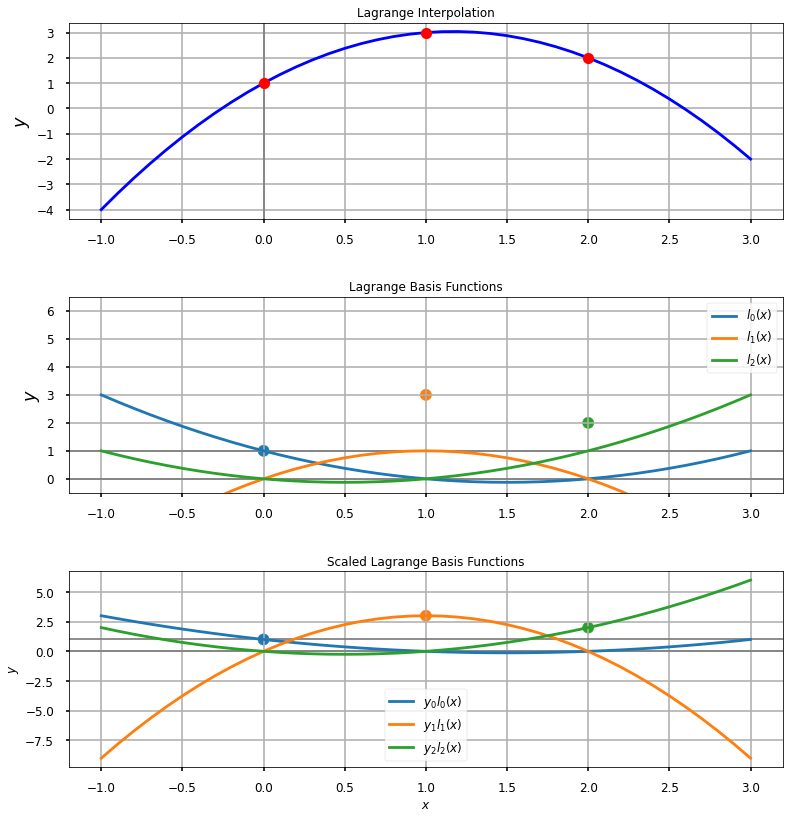
Plot the data and the individual components of the polynomial
x_new = np.arange(-1.0, 3.1, 0.1)
test = lagrange_basis(x, y, x_new)
fig = plt.figure()
fig.subplots_adjust(top=1.3, hspace=0.4)
ax=fig.add_subplot(3,1,1)
ax.axvline(x=0.0, color="grey", linestyle="-", linewidth=1.75)
ax.plot(x_new, f(x_new), 'b', x, y, 'ro')
ax.set_title(r'Lagrange Interpolation', fontsize=12)
ax.grid()
ax.set_ylabel(r'$y$')
ax.tick_params(axis = 'both', which = 'major', labelsize = 12)
ax1=fig.add_subplot(3,1,2)
ax1.axhline(y=0.0, color="grey", linestyle="-", linewidth=1.75)
ax1.axhline(y=1.0, color="grey", linestyle="-", linewidth=1.75)
ax1.scatter(np.array(x), np.array(y), c=['tab:blue', 'tab:orange', 'tab:green'])
ax1.plot(x_new, test[0,:], color='tab:blue', label='$l_0(x)$' )
ax1.plot(x_new, test[1,:], color='tab:orange', label='$l_1(x)$' )
ax1.plot(x_new, test[2,:], color='tab:green', label='$l_2(x)$' )
ax1.set_ylim([-0.5, 6.5])
ax1.grid()
ax1.set_ylabel(r'$y$')
ax1.set_title(r'Lagrange Basis Functions', fontsize=12)
ax1.legend(prop={'size': 12})
ax1.tick_params(axis = 'both', which = 'major', labelsize = 12)
ax2=fig.add_subplot(3,1,3)
ax2.grid()
ax2.axhline(y=0.0, color="grey", linestyle="-", linewidth=1.75)
ax2.axhline(y=1.0, color="grey", linestyle="-", linewidth=1.75)
ax2.scatter(np.array(x), np.array(y), c=['tab:blue', 'tab:orange', 'tab:green'])
ax2.plot(x_new, y[0]*test[0,:], color='tab:blue', label='$y_0 l_0(x)$')
ax2.plot(x_new, y[1]*test[1,:], color='tab:orange', label='$y_1 l_1(x)$' )
ax2.plot(x_new, y[2]*test[2,:], color='tab:green', label='$y_2 l_2(x)$' )
ax2.set_xlabel(r'$x$', fontsize=12)
ax2.set_ylabel(r'$y$', fontsize=12)
ax2.set_title(r'Scaled Lagrange Basis Functions', fontsize=12)
ax2.legend(prop={'size': 12})
ax2.tick_params(axis = 'both', which = 'major', labelsize = 12)
plt.show()
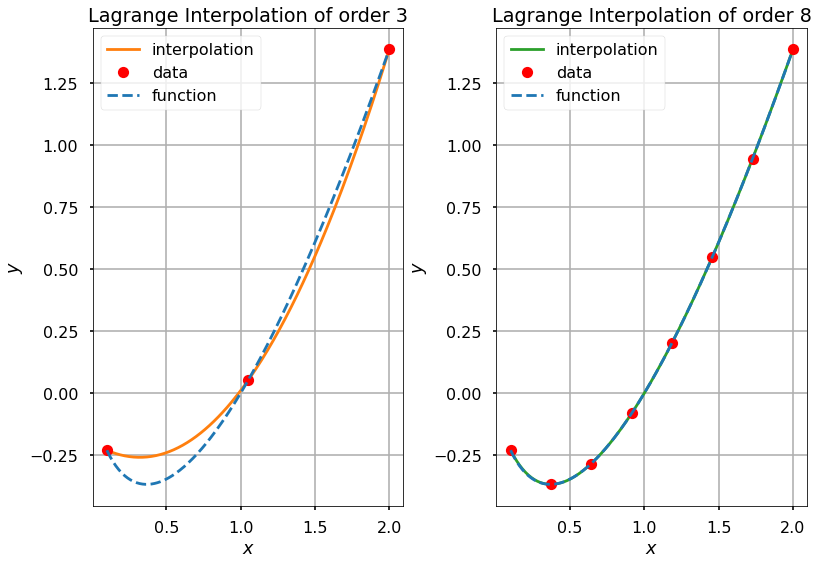
Now use a different set of points, defined by a function $x \log(x)$.
g = lambda x: x * np.log(x)
We can compute the polynomials of different orders and the errors.
m = np.array([3,8])
x0 = 0.1
x1 = 2.0
dx = 0.01
x_new = np.arange(x0, x1, dx)
err = np.zeros( (m.size, x_new.size) )
y_new = np.zeros( (m.size, x_new.size) )
fig1 = plt.figure()
fig1.subplots_adjust(wspace=0.3)
for i in np.arange(m.size):
z = np.linspace(x0, x1, m[i])
y = g(z)
f = lagrange(z, y)
p = Polynomial(f.coef[::-1]).coef
err[i,:] = g(x_new) - f(x_new)
md("Coefficients of the interpolating polynomial: {}".format(p))
ax=fig1.add_subplot(1,m.size,i+1)
clrs = 'tab:orange' if (i==0) else 'tab:green'
ax.plot(x_new, f(x_new), '-', c=clrs, label="interpolation")
ax.plot(z, y, 'ro', label="data")
ax.plot(x_new, np.log(x_new) * x_new, linestyle='--', label="function")
ax.set_title(r'Lagrange Interpolation of order {}'.format(m[i]))
ax.legend()
ax.grid()
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$y$')
plt.show()
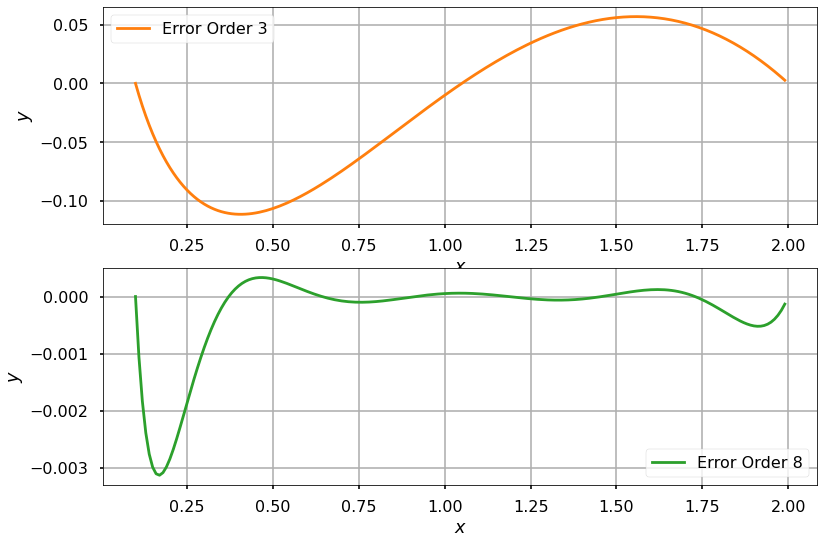
Plot the errors
fig2=plt.figure()
for i in np.arange(m.size):
ax=fig2.add_subplot(m.size,1,i+1)
clrs = 'tab:orange' if (i==0) else 'tab:green'
ax.plot(x_new, err[i], c=clrs, label="Error Order {}".format(m[i]))
ax.legend()
ax.grid()
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$y$')
plt.show()
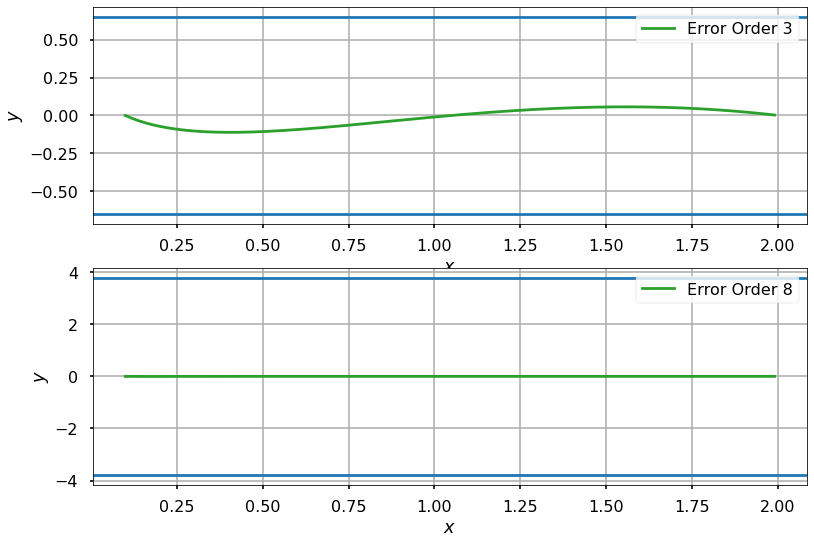
Compute the bounds on the errors.
fig3=plt.figure()
for i in np.arange(m.size):
z = np.linspace(x0, x1, m[i])
bounds1 = np.prod( [(x_new - z[i]) for i in np.arange(0,m[i])], axis=0)
bounds2 = (m[i]-2) * (-1)**(m[i]-2) / ( np.math.factorial(m[i]) * x_new**(m[i]-1) )
ax=fig3.add_subplot(m.size,1,i+1)
b=np.max(np.abs(bounds1 * bounds2))
ax.plot(x_new, err[i], c=clrs, label="Error Order {}".format(m[i]))
ax.axhline(y=b)
ax.axhline(y=-b)
ax.legend()
ax.grid()
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$y$')
plt.show()