Secant Method
import math
import numpy as np
from matplotlib import pyplot as plt
To find maximum of $g(x)$, we need to find roots of $g^{\prime}(x)$, so a can define a function gprime(x)
To find roots and confirm if it is a maxima, we need gdoubleprime(x), as $g(x)$ is at maximum if $g^{\prime\prime}(x)$ is negative
def g(x):
return np.exp(x**2 + 1) - 2.718 + 0.16969*x - 4.07799*x**2 + 3.3653 * x**3 - \
4.1279 * x**4
def gprime(x):
return np.exp(x**2 + 1) * 2 * x + 0.16969 - 2.0 * 4.07799 * x + 3 * 3.3653 * x**2 \
- 4 * 4.1279 * x**3
def gdoubleprime(x):
return 2 * (2 * x + 1) * np.exp(x**2 + 1) - 2.0 * 4.07799 + 3 * 2 * 3.3653 * x \
- 4 * 3 * 4.1279 * x**2
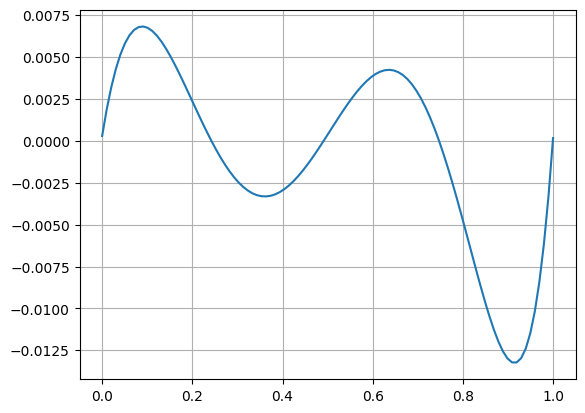
Plot the function over the unit interval
x = np.linspace(0.0, 1.0, 100)
plt.plot(x, g(x))
plt.grid(True)
Newton method
def newton_step(x, step_num):
val = x - gprime(x) / gdoubleprime(x)
step_num += 1
print(f"Step Num: {step_num}, x: {val}")
return val, step_num
Secant method
def secant_step(x1, x2, step_num, f):
step_num += 1
val = x2 - f(x2) * (x2 - x1) / (f(x2) - f(x1))
print(f"Step Num: {step_num}, x: {val}")
return x2, val, step_num
Use secant method here because we can bound it.
def calculate_first_max(x1, x2, nmax = 20):
step_num = 0
for i in range(nmax):
x1, x2, step_num = secant_step(x1, x2, step_num, gprime)
return x2
def calculate_second_max():
step_num = 0
x1 = 0.
x2 = 0.7
for i in range(6):
x1, x2, step_num = secant_step(x1, x2, step_num, gprime)
return x2
print("Calculating x for first maximum in x -> [0, 1], in interval [0, 0.2]:")
max_x_1 = calculate_first_max(0, 0.2, 19)
print("First maximum value: ", g(max_x_1))
Calculating x for first maximum in x -> [0, 1], in interval [0, 0.2]:
Step Num: 1, x: 0.14900380590331655
Step Num: 2, x: -0.08821605866212776
Step Num: 3, x: 0.12814220849590097
Step Num: 4, x: 0.11341387156881519
Step Num: 5, x: 0.0806834268432286
Step Num: 6, x: 0.09017014204250429
Step Num: 7, x: 0.08892692738129448
Step Num: 8, x: 0.08886390723627205
Step Num: 9, x: 0.08886440328278541
Step Num: 10, x: 0.08886440309559314
Step Num: 11, x: 0.08886440309559253
Step Num: 12, x: 0.0888644030955926
Step Num: 13, x: 0.08886440309559303
Step Num: 14, x: 0.08886440309559265
Step Num: 15, x: 0.08886440309559258
Step Num: 16, x: 0.08886440309559261
Step Num: 17, x: 0.0888644030955926
Step Num: 18, x: 0.08886440309559261
Step Num: 19, x: 0.08886440309559261
First maximum value: 0.006812940563426053
print("Calculating x for second maximum in x -> [0, 1], in interval [0.6, 0.7]:")
max_x_2 = calculate_second_max(0.6, 0.7, 6)
print("Second maximum value: ", g(max_x_2))
Calculating x for second maximum in x -> [0, 1], in interval [0.6, 0.7]:
Step Num: 1, x: 0.6307415305490232
Step Num: 2, x: 0.6353034667646523
Step Num: 3, x: 0.6358951723781623
Step Num: 4, x: 0.6358866382102938
Step Num: 5, x: 0.6358866518459403
Step Num: 6, x: 0.6358866518462564
Second maximum value: 0.004225969342977254
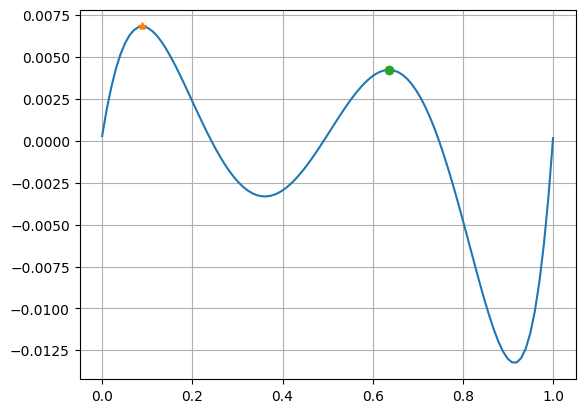
plt.plot(x, g(x))
plt.plot(max_x_1, g(max_x_1), '*')
plt.plot(max_x_2, g(max_x_2), 'o')
plt.grid(True)
