Integrability, Localisation and Bifurcation of an Elastic Conducting Rod in a Uniform Magnetic Field
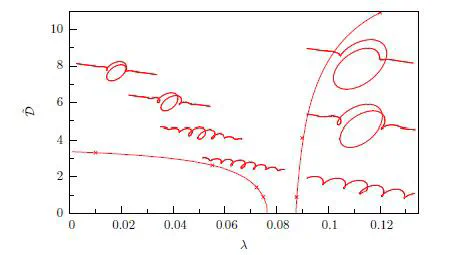 Bifurcation diagram
Bifurcation diagram
The classical problem of the buckling of an elastic rod in a magnetic field is investigated using modern techniques from dynamical systems theory. The Kirchhoff equations, which describe the static equilibrium equations of a geometrically exact rod under end tension and moment are extended by incorporating the evolution of a fixed external vector (in the direction of the magnetic field) that interacts with the rod via a Lorentz force. The static equilibrium equations (in body coordinates) are found to be noncanonical Hamiltonian equations. The Poisson bracket is generalised and the equilibrium equations found to sit, as the third member, in a family of rod equations in generalised magnetic fields. When the rod is linearly elastic, isotropic, inextensible and unshearable the equations are completely integrable and can be generated by a Lax pair.
The isotropic system is reduced using the Casimirs, via the Euler angles, to a four dimensional canonical system with a first integral provided the magnetic field is not aligned with the force within the rod at any point as the system losses rank. An energy surface is specified, defining three-dimensional flows. Poincaré sections then show closed curves.
Through Mel′nikov analysis it is shown that for an extensible rod the presence of a magnetic field leads to the transverse intersection of the stable and unstable manifolds and the loss of complete integrability. Consequently, the system admits spatially chaotic solutions and a multiplicity of multimodal homoclinic solutions exist. Poincaré sections associated with the loss of integrability are displayed. Homoclinic solutions are computed and post-buckling paths found using continuation methods. The rods buckle in a Hamiltonian-Hopf bifurcation about a periodic solution. A codimension-two point, which describes a double Hamiltonian-Hopf bifurcation, determines whether straight rods buckle into localised configurations at either two critical values of the magnetic field, a single critical value or do not buckle at all. The codimension-two point is found to be an organising centre for primary and multimodal solutions.