Integrability of a conducting elastic rod in a magnetic field

Jun 20, 2008·
David Sinden
David Sinden
,
Gert van der Heijden
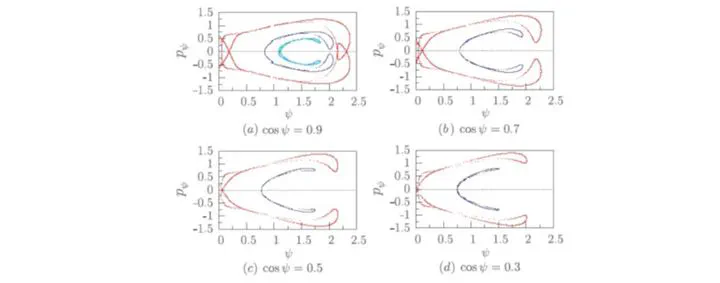Poincare sections showing loss of integrability Poincaré sections
Abstract
We consider the equilibrium equations for a conducting elastic rod placed in a uniform magnetic field, motivated by the problem of electrodynamic space tethers. When expressed in body coordinates the equations are found to sit in a family of non-canonical Hamiltonian systems involving an increasing number of vector fields. These systems, which include the classical Euler and Kirchhoff rods, are shown to be completely integrable in the case of a transversely isotropic rod; they are in fact generated by a Lax pair. For the magnetic rod this gives a physical interpretation to a previously proposed abstract nine-dimensional integrable system. We use the conserved quantities to reduce the equations to a four-dimensional canonical Hamiltonian system, allowing the geometry of the phase space to be investigated through Poincaré sections. In the special case where the force in the rod is aligned with the magnetic field the system turns out to be superintegrable, meaning that the phase space breaks down completely into periodic orbits, corresponding to straight twisted rods.
Type
Publication
J. Phy. A: Math. Theor. 41 045207 (2008)

A preprint can be found on the arxiv.

Update: Jan 2026

The key point is that even in the presence of the Lorentz body force, the rod in a uniform magnetic field is still invariant under a one–parameter family of Euclidean motions, specifically the screw motions whose axis is the magnetic field. Concretely:

  • If you translate the entire rod a little way along the direction of (with no change in its shape) and at the same time rotate each cross-section about the same axis so as to keep the magnetic field fixed in the body–frame, nothing in the energy or in the equilibrium equations changes.

  • By Noether’s theorem this screw–symmetry must produce a conserved momentum map. The corresponding conserved quantity is exactly

    $$ C_1 = \dfrac{1}{2} \boldsymbol{n} \cdot \boldsymbol{n} + \boldsymbol{m} \cdot \boldsymbol{B}. $$

    Thus, $C_1$ is the momentum-map of the one-parameter group of translation-and-rotation symmetries of the uniform–field problem.

The caveat, with no change in its shape is important, as it means that, in the case of the Lorentz body force, inextensibility breaks integrability.

Cosserat
David Sinden
Authors
David Sinden (he/him)
Senior Research Scientist

David Sinden is an applied mathematician working as a senior scientist at the Fraunhofer Institute for Digital Medicine MEVIS, in Bremen.

His research interests include ultrasound modelling, thermal ablation and pharmacokinetic models. He works within the modelling and simulation and image-guided therapy groups.

Authors
gert