Localisation of a twisted conducting rod in a uniform magnetic field: the Hamiltonian-Hopf-Hopf bifurcation
Jun 20, 2011·,
Gert van der Heijden
David Sinden
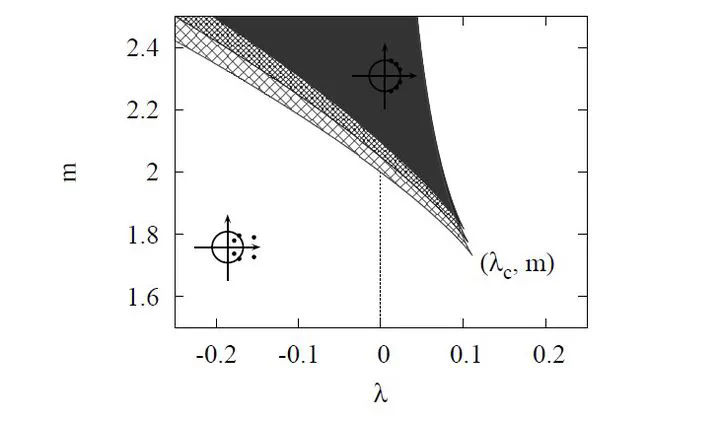Spectrum of monodromy matrixAbstract
We study localised (multi-pulse homoclinic) post-buckling solutions for an extensible conducting rod under end loads and placed in a uniform magnetic field. The homoclinic bifurcation behaviour is found to be organised by a codimension-two Hamiltonian-Hopf-Hopf bifurcation. We predict new stability results for twisted magnetic rods which are relevant for electrodynamic space tethers and potentially for conducting nanowires in future electromechanical devices.
Type
Publication
ENOC 2011
Authors
Authors
David Sinden
(he/him)
Senior Research Scientist
David Sinden is an applied mathematician working as a senior scientist at the Fraunhofer Institute for Digital Medicine MEVIS, in Bremen.
His research interests include ultrasound modelling, thermal ablation and pharmacokinetic models. He works within the modelling and simulation and image-guided therapy groups.