The effects of nonlinear wave propagation on the stability of inertial cavitation
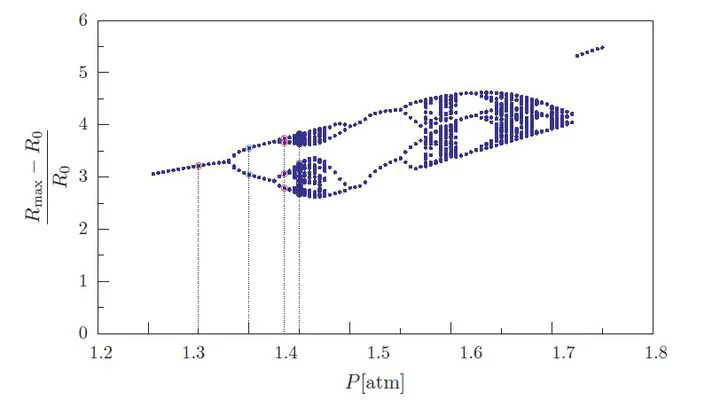 Bifurcation diagram
Bifurcation diagram
Abstract
In the context of forecasting temperature and pressure fields generated by high-intensity focussed ultrasound, the accuracy of predictive models is critical for the safety and efficacy of treatment. In such fields 'inertial' cavitation is often observed. Classically, estimations of cavitation thresholds have been based on the assumption that the incident wave at the surface of a bubble is the same as in the far-field, neglecting the effect of nonlinear wave propagation. By modelling the incident wave as a solution to Burgers' equation using weak shock theory, the effects of nonlinear wave propagation on inertial cavitation are investigated using both numerical and analytical techniques. From radius-time curves for a single bubble, it is observed that there is a reduction in the maximum size of a bubble undergoing inertial cavitation and that the inertial collapse occurs earlier in contrast with the classical case. Corresponding stability thresholds for a bubble whose initial radius is slightly below the critical Blake radius are calculated, providing a lower bound for the onset of instability. Bifurcation diagrams and frequency-response curves are presented associated with the loss of stability. The consequences and physical implications of the results are discussed with respect to the classical results.
Type
Publication
Journal of Physics: Conference Series