Spatial chaos of an extensible conducting rod in a uniform magnetic field
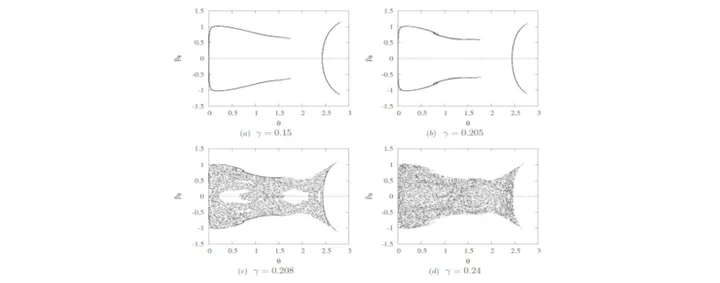Poincaré sections
Abstract
The equilibrium equations for the isotropic Kirchhoff rod are known to form an integrable system. It is also known that the effects of extensibility and shearability of the rod do not break the integrable structure. Nor, as we have shown in a previous paper does the effect of a magnetic field on a conducting rod. Here we show, by means of Mel′nikov analysis, that, interestingly, the combined effects do destroy integrability; that is, the governing equations for an extensible current-carrying rod in a uniform magnetic field are nonintegrable. This result has implications for possible configurations of electrodynamic space tethers and may be relevant for electromechanical devices.
Type
Publication
Journal of Physics A: Mathematical and Theoretical
A preprint can be found on the arxiv.
